Yes, by cutting face down.
(laser theory follows)
There is no way to get a inverted kerf profile with the glowforge, focus height won’t do it, nothing will. It’s all down to the physics of the laser and the circular cross section of the light beam.
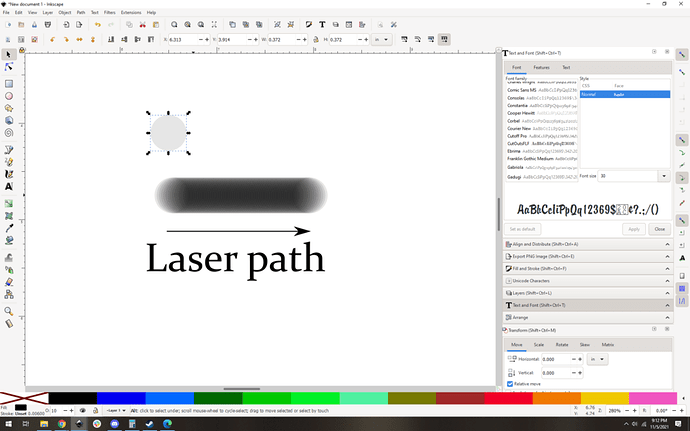
It can help to think of it like a series of “dots” of light. You can model it pretty effectively with semitransparent circles in your favorite image editor:
Imagine the laser is a circle of uniform light density (it is, mostly), you get this sort of arragement. The one circle at the top is a representative laser beam. As you run that beam left to right, the “circles” overlap and you get a natural gradient of how much light is hitting the material as the laser travels:
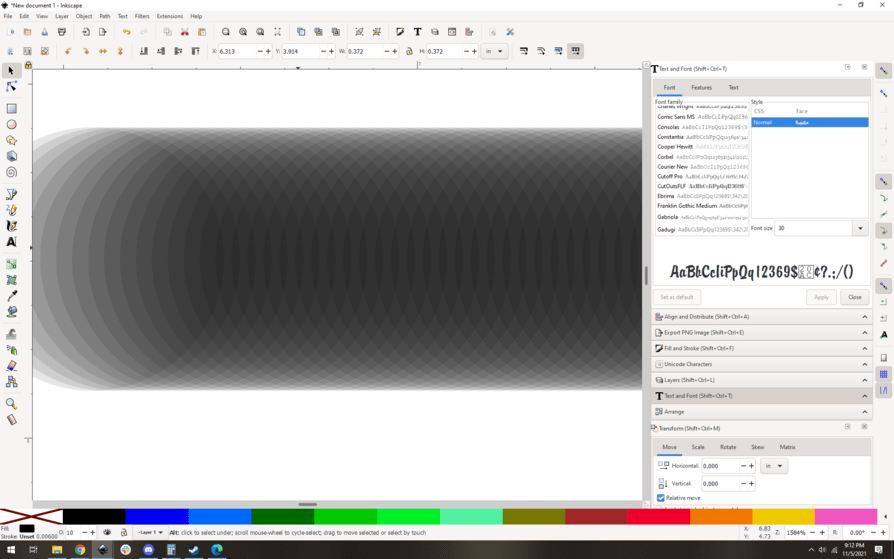
Zooming in it’s easier to see:
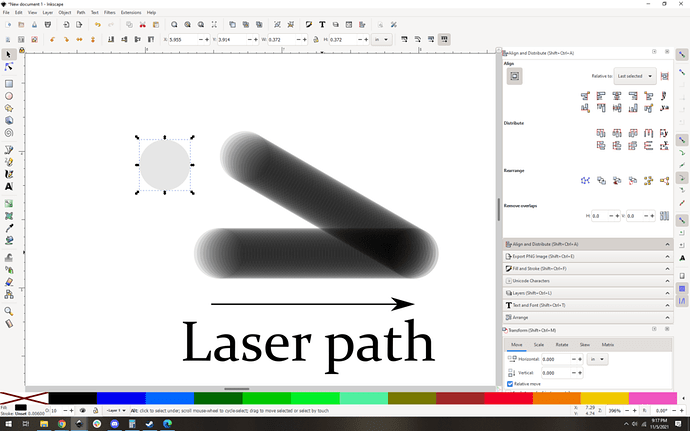
You can see that the amount of power that hits the material drops off on the edges of the laser path. The top and bottom are lighter, which is roughly our model for how much laser energy is actually being applied. Also of interest is the ends of the paths, they get significantly less energy. Sharp corners get a lot more, check it out:
That significant overlap plus the acceleration effects that make constant speed through corners impossible was a tricky thing for glowforge to improve… they worked hard on this problem to get what they call “clean corners”.
Anyway, long story short, the center of the path always gets more laser energy, and so it’ll always be “deeper”. This effect outweighs the hourglass shape of the beam, as that is very slight 1. Since you’re trying to just barely cut through, you will always notice an angled cut profile. Physics!
And we even have empirical evidence to bear it out, from @kittski:
So, case seems pretty closed, yeah?
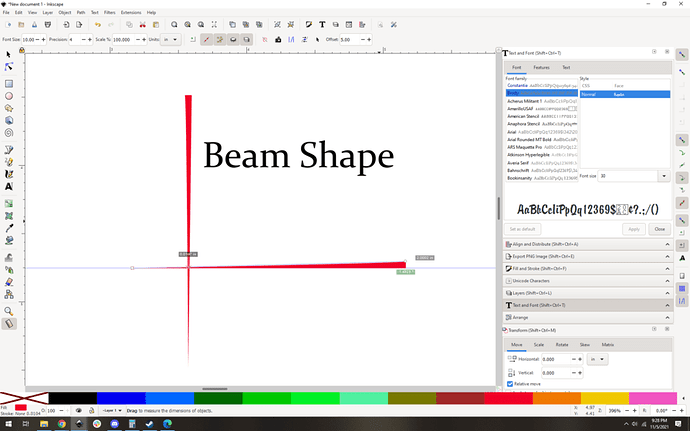
1 We can calculate the hourglass angle. From this post, we see that the beam is about 0.05" wide without a lens. The lens height above the tray is roughly 2 inches, so that leaves us with this sort of arrangement: You can see that the rough angle of the hourglass (represented by the red triangle) is about 1.4 degrees or 0.7 degrees for each side. That’s less than the observed kerf angle, so the hourglass can’t really reverse it even in ideal conditions.
Supporting research:
Extreme width scoring